PCA: Regressione¶
Cosa andremo a fare oggi?¶
Creazione di un dataset usando la libreria pandas. Come passare da numpy array to pandas dataframe
Scikit-Learn datasets Spiegazione, nozioni su come scaricarli applicazione della regressione lineare a un dataset di scikit-learn (diabetes dataset)
Cosa significa correlazione? Quando e perchè si utilizza
Principal Component Analysis (PCA) dimensionality reduction
Riduzione del numero di input a un numero fisso (es. 2)
Come facciamo a riddure il numero degli input senza ridurre il contenuto di informazioni del nostro dataset iniziale?
Esempio pratico: Regressione lineare applicata a un dataset con e senza PCA.
Creazione di un dataset usando la libreria pandas¶
In questo paragrafo andiamo a vedere come creare una classe dataset usando sia numpy che pandas in modo che possiamo facilmente applicare le regressioni studiate a questo. Inoltre vedremo come utilizare i dataset di scikit-learn.
'''
Y = Salario al mese in euro
X1 = Età del lavoratore
X2 = Numero di ore mensili di lavoro
X3 = Indice di esperienza da 1 a 10
Equazione = Y = w0 + w1*X1 + w2*X2 + w3*X3
1) Marco: Y=1100 X1=19 X2=150 X3=6 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*19 + w2*150 + w3*6
2) Daniele: Y=1150 X1=21 X2=135 X3=8 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*21 + w2*135 + w3*8
3) Davide: Y=1155 X1=22 X2=160 X3=5 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*22 + w2*160 + w3*5
4) Marta: Y=1170 X1=23 X2=158 X3=7 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*23 + w2*158 + w3*7
6) Alessia: Y=1200 X1=26 X2=155 X3=7 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*26 + w2*155 + w3*7
9) Stella: Y=1750 X1=33 X2=120 X3=10 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*33 + w2*120 + w3*10
10) Chiara Y=1640 X1=29 X2=130 x3=9 Y= w0*1 + w1*X1 + w2*X2 + w3*X3 --> 1100 = w0*1 + w1*29 + w2*130 + w3*9
'''
import pandas as pd
class Dataset():
def __init__(self):
self.X = np.array([[19,150,6],[21,135,8], [22,160,5], [23,158,7], [26,155,7], [33,120,10],[29,130,9]])
self.Y = np.array([[1100],[1150],[1155],[1170],[1200],[1750],[1640]])
def createPandasDataset(self):
df_X = pd.DataFrame(data=self.X, columns =["età","ore mensili", "esperienza"])
df_Y = pd.DataFrame(data=self.Y, columns =["salario"])
return df_X, df_Y
myDataset = Dataset()
df_X, df_Y = myDataset.createPandasDataset()
display(df_X)
display(df_Y)
| età | ore mensili | esperienza | |
|---|---|---|---|
| 0 | 19 | 150 | 6 |
| 1 | 21 | 135 | 8 |
| 2 | 22 | 160 | 5 |
| 3 | 23 | 158 | 7 |
| 4 | 26 | 155 | 7 |
| 5 | 33 | 120 | 10 |
| 6 | 29 | 130 | 9 |
| solario | |
|---|---|
| 0 | 1100 |
| 1 | 1150 |
| 2 | 1155 |
| 3 | 1170 |
| 4 | 1200 |
| 5 | 1750 |
| 6 | 1640 |
Scikit-Learn datasets spiegazione e nozioni su come scaricarli.¶
Andremo a vedere quali dataset sono disponibili in scikit-learn, come scaricarli e capirne il contenuto.
I dataset disponibili sono i seguenti:
Regressione:
Classificazione:
Implementazione di una classe capace di scaricare i dati da scikit-learn, visualizzarli e analizzarli.
# Importare i datasets
from sklearn import datasets
import pandas as pd
class ScikitLearnDatasets:
def __init__(self, dataset_name):
# Load all scikit-learn dataset
if ("iris"==dataset_name):
self.dataset_scelto = datasets.load_iris() # Classificazione iris dataset
elif ("digits"==dataset_name):
self.dataset_scelto = datasets.load_digits() # Classificazione Load digits dataset
elif ("wine"==dataset_name):
self.dataset_scelto = datasets.load_wine() # Classificazione Load wine dataset
elif ("breast_cancer"==dataset_name):
self.dataset_scelto = datasets.load_breast_cancer() # Classificazione Load breast_cancer dataset
elif ("boston"==dataset_name):
self.dataset_scelto = datasets.load_boston() # Regressione Load boston dataset
self.dataset_scelto.update([ ('target_names', ['Boston-House-Price'])] )
elif ("diabetes"==dataset_name):
self.dataset_scelto = datasets.load_diabetes() # Regressione Load diabetes dataset
self.dataset_scelto.update([ ('target_names', ['Desease-Progression'])] )
elif ("linnerud"==dataset_name):
self.dataset_scelto = datasets.load_linnerud() # Regressione Load linnerud dataset
else:
self.dataset_scelto = diabetes # Regressione default choice
# Print dataset information
self.printDatasetInformation()
def printDatasetInformation(self):
#print(dataset_scelto)
parametri = self.dataset_scelto.keys()
valore = self.dataset_scelto.values()
print(parametri)
# Print useful information
for name in parametri:
print("------------------------------------------")
print(name , self.dataset_scelto[name])
print("------------------------------------------")
def getXY(self):
# Get Input (X) Data
X = self.dataset_scelto['data'] # or data = iris.get('data')
X_names = self.dataset_scelto['feature_names']
# Get Output (Y) Target
parametri = self.dataset_scelto.keys()
Y = self.dataset_scelto['target']
Y_names = self.dataset_scelto['target_names']
print("Dataset Parameters: ", parametri)
print("Feature Names: ", X_names)
print("Output Names: ", Y_names)
print("Input X Shape: " , X.shape)
print("Output Y Shape: " , Y.shape)
return X,Y,X_names,Y_names
def createPandasDataFrame(self,X,Y,X_names,Y_names,dataset_name):
df_X = pd.DataFrame(data=X, columns =X_names)
df_Y = pd.DataFrame(data=Y, columns =Y_names)
return df_X, df_Y
def writeDataFrameToCsv(self,df_X,df_Y):
# Create csv file
df_X.to_csv(dataset_name + '_X.csv', sep = ',', index = False)
df_Y.to_csv(dataset_name + '_Y.csv', sep = ',', index = False)
# Choose the dataset
# Regressione: "boston", "diabetes",
# Classificazione: "iris", "digits", "wine", "breast_cancer "
# Regressione: "diabetes", "boston", "linnerud"
dataset_name = "diabetes"
myScikitLearnDatasets=ScikitLearnDatasets(dataset_name)
X,Y,X_names,Y_names = myScikitLearnDatasets.getXY()
df_X,df_Y = myScikitLearnDatasets.createPandasDataFrame(X,Y,X_names,Y_names,dataset_name)
myScikitLearnDatasets.writeDataFrameToCsv(df_X,df_Y)
display(df_X)
display(df_Y)
dict_keys(['data', 'target', 'DESCR', 'feature_names', 'data_filename', 'target_filename', 'target_names'])
------------------------------------------
data [[ 0.03807591 0.05068012 0.06169621 ... -0.00259226 0.01990842
-0.01764613]
[-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
-0.09220405]
[ 0.08529891 0.05068012 0.04445121 ... -0.00259226 0.00286377
-0.02593034]
...
[ 0.04170844 0.05068012 -0.01590626 ... -0.01107952 -0.04687948
0.01549073]
[-0.04547248 -0.04464164 0.03906215 ... 0.02655962 0.04452837
-0.02593034]
[-0.04547248 -0.04464164 -0.0730303 ... -0.03949338 -0.00421986
0.00306441]]
------------------------------------------
------------------------------------------
target [151. 75. 141. 206. 135. 97. 138. 63. 110. 310. 101. 69. 179. 185.
118. 171. 166. 144. 97. 168. 68. 49. 68. 245. 184. 202. 137. 85.
131. 283. 129. 59. 341. 87. 65. 102. 265. 276. 252. 90. 100. 55.
61. 92. 259. 53. 190. 142. 75. 142. 155. 225. 59. 104. 182. 128.
52. 37. 170. 170. 61. 144. 52. 128. 71. 163. 150. 97. 160. 178.
48. 270. 202. 111. 85. 42. 170. 200. 252. 113. 143. 51. 52. 210.
65. 141. 55. 134. 42. 111. 98. 164. 48. 96. 90. 162. 150. 279.
92. 83. 128. 102. 302. 198. 95. 53. 134. 144. 232. 81. 104. 59.
246. 297. 258. 229. 275. 281. 179. 200. 200. 173. 180. 84. 121. 161.
99. 109. 115. 268. 274. 158. 107. 83. 103. 272. 85. 280. 336. 281.
118. 317. 235. 60. 174. 259. 178. 128. 96. 126. 288. 88. 292. 71.
197. 186. 25. 84. 96. 195. 53. 217. 172. 131. 214. 59. 70. 220.
268. 152. 47. 74. 295. 101. 151. 127. 237. 225. 81. 151. 107. 64.
138. 185. 265. 101. 137. 143. 141. 79. 292. 178. 91. 116. 86. 122.
72. 129. 142. 90. 158. 39. 196. 222. 277. 99. 196. 202. 155. 77.
191. 70. 73. 49. 65. 263. 248. 296. 214. 185. 78. 93. 252. 150.
77. 208. 77. 108. 160. 53. 220. 154. 259. 90. 246. 124. 67. 72.
257. 262. 275. 177. 71. 47. 187. 125. 78. 51. 258. 215. 303. 243.
91. 150. 310. 153. 346. 63. 89. 50. 39. 103. 308. 116. 145. 74.
45. 115. 264. 87. 202. 127. 182. 241. 66. 94. 283. 64. 102. 200.
265. 94. 230. 181. 156. 233. 60. 219. 80. 68. 332. 248. 84. 200.
55. 85. 89. 31. 129. 83. 275. 65. 198. 236. 253. 124. 44. 172.
114. 142. 109. 180. 144. 163. 147. 97. 220. 190. 109. 191. 122. 230.
242. 248. 249. 192. 131. 237. 78. 135. 244. 199. 270. 164. 72. 96.
306. 91. 214. 95. 216. 263. 178. 113. 200. 139. 139. 88. 148. 88.
243. 71. 77. 109. 272. 60. 54. 221. 90. 311. 281. 182. 321. 58.
262. 206. 233. 242. 123. 167. 63. 197. 71. 168. 140. 217. 121. 235.
245. 40. 52. 104. 132. 88. 69. 219. 72. 201. 110. 51. 277. 63.
118. 69. 273. 258. 43. 198. 242. 232. 175. 93. 168. 275. 293. 281.
72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257. 55. 84. 42.
146. 212. 233. 91. 111. 152. 120. 67. 310. 94. 183. 66. 173. 72.
49. 64. 48. 178. 104. 132. 220. 57.]
------------------------------------------
------------------------------------------
DESCR .. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
**Data Set Characteristics:**
:Number of Instances: 442
:Number of Attributes: First 10 columns are numeric predictive values
:Target: Column 11 is a quantitative measure of disease progression one year after baseline
:Attribute Information:
- Age
- Sex
- Body mass index
- Average blood pressure
- S1
- S2
- S3
- S4
- S5
- S6
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
------------------------------------------
------------------------------------------
feature_names ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
------------------------------------------
------------------------------------------
data_filename /usr/local/lib/python3.6/dist-packages/sklearn/datasets/data/diabetes_data.csv.gz
------------------------------------------
------------------------------------------
target_filename /usr/local/lib/python3.6/dist-packages/sklearn/datasets/data/diabetes_target.csv.gz
------------------------------------------
------------------------------------------
target_names ['Desease-Progression']
------------------------------------------
Dataset Parameters: dict_keys(['data', 'target', 'DESCR', 'feature_names', 'data_filename', 'target_filename', 'target_names'])
Feature Names: ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
Output Names: ['Desease-Progression']
Input X Shape: (442, 10)
Output Y Shape: (442,)
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 437 | 0.041708 | 0.050680 | 0.019662 | 0.059744 | -0.005697 | -0.002566 | -0.028674 | -0.002592 | 0.031193 | 0.007207 |
| 438 | -0.005515 | 0.050680 | -0.015906 | -0.067642 | 0.049341 | 0.079165 | -0.028674 | 0.034309 | -0.018118 | 0.044485 |
| 439 | 0.041708 | 0.050680 | -0.015906 | 0.017282 | -0.037344 | -0.013840 | -0.024993 | -0.011080 | -0.046879 | 0.015491 |
| 440 | -0.045472 | -0.044642 | 0.039062 | 0.001215 | 0.016318 | 0.015283 | -0.028674 | 0.026560 | 0.044528 | -0.025930 |
| 441 | -0.045472 | -0.044642 | -0.073030 | -0.081414 | 0.083740 | 0.027809 | 0.173816 | -0.039493 | -0.004220 | 0.003064 |
442 rows × 10 columns
| Desease-Progression | |
|---|---|
| 0 | 151.0 |
| 1 | 75.0 |
| 2 | 141.0 |
| 3 | 206.0 |
| 4 | 135.0 |
| ... | ... |
| 437 | 178.0 |
| 438 | 104.0 |
| 439 | 132.0 |
| 440 | 220.0 |
| 441 | 57.0 |
442 rows × 1 columns
Cosa significa correlazione?¶
Andiamo a vedere come si interpreta la matrice di correlazione. Rispondiamo alla domanda:
Come deve essere la matrice di correlazione?
import matplotlib.pyplot as plt
# Correlation Matrix
plt.matshow(df_X.corr())
plt.xticks(range(len(df_X.columns)), df_X.columns)
plt.yticks(range(len(df_X.columns)), df_X.columns)
plt.colorbar()
plt.show()
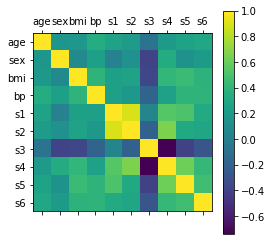
df_X.corr().style.background_gradient(cmap='coolwarm').set_precision(2)
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| age | 1 | 0.17 | 0.19 | 0.34 | 0.26 | 0.22 | -0.075 | 0.2 | 0.27 | 0.3 |
| sex | 0.17 | 1 | 0.088 | 0.24 | 0.035 | 0.14 | -0.38 | 0.33 | 0.15 | 0.21 |
| bmi | 0.19 | 0.088 | 1 | 0.4 | 0.25 | 0.26 | -0.37 | 0.41 | 0.45 | 0.39 |
| bp | 0.34 | 0.24 | 0.4 | 1 | 0.24 | 0.19 | -0.18 | 0.26 | 0.39 | 0.39 |
| s1 | 0.26 | 0.035 | 0.25 | 0.24 | 1 | 0.9 | 0.052 | 0.54 | 0.52 | 0.33 |
| s2 | 0.22 | 0.14 | 0.26 | 0.19 | 0.9 | 1 | -0.2 | 0.66 | 0.32 | 0.29 |
| s3 | -0.075 | -0.38 | -0.37 | -0.18 | 0.052 | -0.2 | 1 | -0.74 | -0.4 | -0.27 |
| s4 | 0.2 | 0.33 | 0.41 | 0.26 | 0.54 | 0.66 | -0.74 | 1 | 0.62 | 0.42 |
| s5 | 0.27 | 0.15 | 0.45 | 0.39 | 0.52 | 0.32 | -0.4 | 0.62 | 1 | 0.46 |
| s6 | 0.3 | 0.21 | 0.39 | 0.39 | 0.33 | 0.29 | -0.27 | 0.42 | 0.46 | 1 |
import seaborn as sns
corr = df_X.corr()
sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values)
<matplotlib.axes._subplots.AxesSubplot at 0x7f3407ea9320>

Dimensionality Reduction (Principal Component Analysis PCA)¶
Nel caso vi sia una situazione in cui la correlazione tra le features è molto alta possiamo sia manualmente rimuovere le feature che consideriamo superflue oppure utilizzare la PCA. Quest’ultima si occupa di creare nuove features (se prima ne avevamo 10 adesso ne avremo un numero minore) che non hanno un significato fisico ma che sono sufficienti a rappresentare il nostro dataset. In poche parole semplichiamo gli input (features) al minimo numero necessario. Questò fara si che tra gli input vi sia pochissima correlazione in quanto ogni input features avrà un valore diverso dalle altre.
IMPORTANTE: Il calcolo della principal componet analysis (PCA) è fortemente influenzato dalla scala. Quindi è necesseria avere per tutti gli input (features ) una scala comune.
Standardizzare i dati significarli ricondurli a una scala il cui mean=0 e la variance=1.
from sklearn.preprocessing import StandardScaler
features = X_names
# Separating out the features
x = df_X
# Separating out the target
y = df_Y
# Standardizing the features
x = StandardScaler().fit_transform(x)
df_X_Standard = pd.DataFrame(data = x , columns = X_names)
display(df_X)
display(df_X_Standard)
df_X.keys()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 437 | 0.041708 | 0.050680 | 0.019662 | 0.059744 | -0.005697 | -0.002566 | -0.028674 | -0.002592 | 0.031193 | 0.007207 |
| 438 | -0.005515 | 0.050680 | -0.015906 | -0.067642 | 0.049341 | 0.079165 | -0.028674 | 0.034309 | -0.018118 | 0.044485 |
| 439 | 0.041708 | 0.050680 | -0.015906 | 0.017282 | -0.037344 | -0.013840 | -0.024993 | -0.011080 | -0.046879 | 0.015491 |
| 440 | -0.045472 | -0.044642 | 0.039062 | 0.001215 | 0.016318 | 0.015283 | -0.028674 | 0.026560 | 0.044528 | -0.025930 |
| 441 | -0.045472 | -0.044642 | -0.073030 | -0.081414 | 0.083740 | 0.027809 | 0.173816 | -0.039493 | -0.004220 | 0.003064 |
442 rows × 10 columns
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.800500 | 1.065488 | 1.297088 | 0.459840 | -0.929746 | -0.732065 | -0.912451 | -0.054499 | 0.418551 | -0.370989 |
| 1 | -0.039567 | -0.938537 | -1.082180 | -0.553511 | -0.177624 | -0.402886 | 1.564414 | -0.830301 | -1.436551 | -1.938479 |
| 2 | 1.793307 | 1.065488 | 0.934533 | -0.119218 | -0.958674 | -0.718897 | -0.680245 | -0.054499 | 0.060207 | -0.545154 |
| 3 | -1.872441 | -0.938537 | -0.243771 | -0.770658 | 0.256292 | 0.525397 | -0.757647 | 0.721302 | 0.477072 | -0.196823 |
| 4 | 0.113172 | -0.938537 | -0.764944 | 0.459840 | 0.082726 | 0.327890 | 0.171178 | -0.054499 | -0.672582 | -0.980568 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 437 | 0.876870 | 1.065488 | 0.413360 | 1.256044 | -0.119769 | -0.053957 | -0.602843 | -0.054499 | 0.655795 | 0.151508 |
| 438 | -0.115937 | 1.065488 | -0.334410 | -1.422098 | 1.037341 | 1.664355 | -0.602843 | 0.721302 | -0.380915 | 0.935254 |
| 439 | 0.876870 | 1.065488 | -0.334410 | 0.363330 | -0.785107 | -0.290965 | -0.525441 | -0.232934 | -0.985585 | 0.325674 |
| 440 | -0.956004 | -0.938537 | 0.821235 | 0.025547 | 0.343075 | 0.321306 | -0.602843 | 0.558384 | 0.936155 | -0.545154 |
| 441 | -0.956004 | -0.938537 | -1.535374 | -1.711626 | 1.760535 | 0.584649 | 3.654268 | -0.830301 | -0.088717 | 0.064426 |
442 rows × 10 columns
Index(['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6'], dtype='object')
Riduciamo il numero delle features (input) a 2 usando la PCA¶
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents , columns = ['principal component 1', 'principal component 2'])
display(principalDf)
# Varianza associata ad ogni componente
pca.explained_variance_ratio_
| principal component 1 | principal component 2 | |
|---|---|---|
| 0 | 0.587208 | -1.946828 |
| 1 | -2.831612 | 1.372085 |
| 2 | 0.272148 | -1.634898 |
| 3 | 0.049310 | 0.382253 |
| 4 | -0.756451 | 0.811968 |
| ... | ... | ... |
| 437 | 1.239531 | -1.035955 |
| 438 | 1.264676 | 0.761301 |
| 439 | -0.205246 | -1.205446 |
| 440 | 0.692866 | 0.210117 |
| 441 | -1.903934 | 3.975771 |
442 rows × 2 columns
array([0.40242142, 0.14923182])
Dobbiamo capire il levello di informazione di ogni singola componente trovata. Quando riduciamo la dimensionalità perdiamo delle informazioni in quanto il numero di input è stato ridotto. Vogliamo chiederci adesso le componenti 1 e 2 quanta informazione contengono? La compomente 1 contiene il 40% della varianza mentre la componete 2 il 14 %. Insieme essi contengono il 54% della varianza. Cioè significa che rispetto alle informazioni iniziali abbiamo perso il 46%.
Come facciamo a riddure il numero degli input senza ridurre il contenuto di informazioni del nostro dataset iniziale?¶
Mantenere esattamente il 100 % delle informazioni è impossibile. Pertanto ridurremo di poco il contenuto delle informazioni (es. 90%). Questo ci permetterà di ridurre il numero di input ed avere allo stesso tempo un predizione ottima.
from sklearn.decomposition import PCA
# If 0 < n_components < 1 and svd_solver == 'full', select the number of
# components such that the amount of variance that needs to be explained
# is greater than the percentage specified by n_components.
pca = PCA(n_components=0.90)
x = df_X.values
x = StandardScaler().fit_transform(x)
principalComponents = pca.fit_transform(x)
row_number = principalComponents.shape[1]
X_names_new = []
for i in range(0,row_number):
name = "component_" + str(i)
X_names_new.append(name)
principalDf = pd.DataFrame(data = principalComponents ,columns=X_names_new)
display(principalDf)
# Varianza associata ad ogni componente
variance_arr = pca.explained_variance_ratio_
tot_variance = 0
for variance in variance_arr:
temp_variance = variance*100
tot_variance += temp_variance
print(tot_variance)
| component_0 | component_1 | component_2 | component_3 | component_4 | component_5 | component_6 | |
|---|---|---|---|---|---|---|---|
| 0 | 0.587208 | -1.946828 | 0.589233 | -0.082812 | -0.256630 | -1.011214 | -0.179807 |
| 1 | -2.831612 | 1.372085 | 0.027915 | -0.469999 | -0.143229 | -1.013015 | 0.224414 |
| 2 | 0.272148 | -1.634898 | 0.739270 | -0.791475 | -1.163821 | -1.112806 | -0.462406 |
| 3 | 0.049310 | 0.382253 | -2.013037 | 1.373239 | 0.255528 | 0.445315 | 0.482147 |
| 4 | -0.756451 | 0.811968 | -0.057259 | -0.137520 | -0.133344 | -0.814591 | 0.436451 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 437 | 1.239531 | -1.035955 | 0.928691 | -0.656266 | 0.204315 | -0.479371 | 0.394431 |
| 438 | 1.264676 | 0.761301 | -1.750210 | -1.133482 | -0.094014 | 0.973430 | -1.173570 |
| 439 | -0.205246 | -1.205446 | 0.496078 | -1.353349 | -0.141686 | -0.045289 | -0.635451 |
| 440 | 0.692866 | 0.210117 | -0.868730 | 1.616790 | 0.119649 | -0.556900 | 0.545703 |
| 441 | -1.903934 | 3.975771 | -0.048381 | -0.220612 | 0.599824 | 1.647108 | 0.245265 |
442 rows × 7 columns
94.79436357350414
Esempio Pratico¶
Scarichiamo il boston dataset
Dividiamo i dati in training e test
Applichiamo la PCA
Compariamo la predizione di un Regressore Lineare con e senza pca
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
import os
from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
plt.rcParams['figure.figsize'] = [15, 10]
# FUNCTION: Standard data with 0 mean and unit variance (Gaussian)
def standardScaler(df):
# Input pandas dataframe Output pandas dataframe scaled
names = list(df.keys())
data = df.values
data_scaled = StandardScaler().fit_transform(data)
df_scaled = pd.DataFrame(data = data_scaled , columns=names)
#print(df)
#print(df_scaled)
return df_scaled
# FUNCTION: Create pandas dataframe from numpy array
def createPandasDataFrame(X,Y,X_names,Y_names):
df_X = pd.DataFrame(data=X, columns =X_names)
df_Y = pd.DataFrame(data=Y, columns =Y_names)
return df_X, df_Y
# FUNCTION: Write pandas dataframe to csv file
def writeDataFrameToCsv(df_X,df_Y,directory_path,dataset_name):
if not os.path.exists(directory_path):
os.makedirs(directory_path)
# Create csv file
path_write = os.path.join(directory_path, dataset_name)
df_X.to_csv(path_write + '_X.csv', sep = ',', index = False)
df_Y.to_csv(path_write + '_Y.csv', sep = ',', index = False)
# FUNCTION: Read from csv file a dataset
def readDataFrameFromCsv(directory_path, dataset_name):
path_read = os.path.join(directory_path, dataset_name)
if not os.path.exists(directory_path):
print("Directory path does not exist")
df_X = pd.read_csv(path_read + '_X.csv')
df_Y = pd.read_csv(path_read + '_Y.csv')
return df_X, df_Y
# CLASS: PCA class to do input dimensionality reduction
class dimensionalityReduction():
def __init__(self,n_components):
# define pca
self.pca = PCA(n_components)
def create_names(self,col_number):
names = []
for i in range(0,col_number):
name = "component_" + str(i)
names.append(name)
return names
def fit(self,df):
df_scaled = standardScaler(df)
model = self.pca.fit(df_scaled.values)
information_array = model.explained_variance_ratio_ *100.00
total_information = np.sum(information_array)
return model,information_array, total_information
def transform(self, model,df):
# Input dataframe
principalComponents = model.transform(df.values)
names = self.create_names(col_number=principalComponents.shape[1])
df_scaled = pd.DataFrame(data = principalComponents , columns = names)
return df_scaled
# CLASS: Easily import different datasets
class ScikitLearnDatasets():
def __init__(self, dataset_name):
# Load all scikit-learn dataset
if ("iris"==dataset_name):
self.dataset_scelto = datasets.load_iris() # Classificazione iris dataset
elif ("digits"==dataset_name):
self.dataset_scelto = datasets.load_digits() # Classificazione Load digits dataset
elif ("wine"==dataset_name):
self.dataset_scelto = datasets.load_wine() # Classificazione Load wine dataset
elif ("breast_cancer"==dataset_name):
self.dataset_scelto = datasets.load_breast_cancer() # Classificazione Load breast_cancer dataset
elif ("boston"==dataset_name):
self.dataset_scelto = datasets.load_boston() # Regressione Load boston dataset
self.dataset_scelto.update([ ('target_names', ['Boston-House-Price'])] )
elif ("diabetes"==dataset_name):
self.dataset_scelto = datasets.load_diabetes() # Regressione Load diabetes dataset
self.dataset_scelto.update([ ('target_names', ['Desease-Progression'])] )
elif ("linnerud"==dataset_name):
self.dataset_scelto = datasets.load_linnerud() # Regressione Load linnerud dataset
else:
self.dataset_scelto = "diabetes" # Regressione default choice
# Print dataset information
#self.printDatasetInformation()
def printDatasetInformation(self):
#print(dataset_scelto)
parameters = self.dataset_scelto.keys()
data = self.dataset_scelto.values()
#print(parameters)
# Print useful information
for name in parameters:
print("------------------------------------------")
print(name , self.dataset_scelto[name])
print("------------------------------------------")
def getXY(self):
# Get Input (X) Data
X = self.dataset_scelto['data'] # or data = iris.get('data')
X_names = self.dataset_scelto['feature_names']
# Get Output (Y) Target
parameters = self.dataset_scelto.keys()
Y = self.dataset_scelto['target']
Y_names = self.dataset_scelto['target_names']
return X,Y,X_names,Y_names
# CLASS: Linar Regression
class LinearRegression():
def __init__(self):
# Inizializzazione
# https://scikit-learn.org/stable/modules/linear_model.html#ridge-regression-and-classification
self.model = linear_model.LinearRegression(fit_intercept=True, normalize=False)
def train(self,X,Y):
# Stimare w0, w1 .. wN
trained_model = self.model.fit(X,Y)
#print("w1,w2 .. wN : ",self.model.coef_)
#print("w0 : ", self.model.intercept_)
return trained_model
def predict(self,X_test,trained_model):
Y_pred = trained_model.predict(X_test)
return Y_pred
def evaluate(self,X_test, Y_test, trained_model):
# R2 score
Y_pred = trained_model.predict(X_test)
R2_score = trained_model.score(X_test, Y_test)
RMSE_score = (np.sqrt(mean_squared_error(Y_test, Y_pred)))
return Y_pred,R2_score, RMSE_score
def plot(self,Y_test,Y_pred):
length = Y_pred.shape[0] # 20
index_bar = np.linspace(0,length,length)
plt.plot(index_bar, Y_test, label='Test')
plt.plot(index_bar, Y_pred, label='Prediction')
plt.legend()
plt.show()
if __name__ == "__main__":
# ----------- SKLEARN DATASET LOADING ------------ #
# Load sklearn dataset
# Classificazione: "iris", "digits", "wine", "breast_cancer "
# Regressione: "diabetes", "boston", "linnerud"
# 1. Select dataset
dataset_name = "diabetes"
# 2. Create class object ScikitLearnDatasets
myScikitLearnDatasets=ScikitLearnDatasets(dataset_name)
# 3. Print dataset information
#myScikitLearnDatasets.printDatasetInformation()
# 4. Get dataset data as numpy array X=input, Y=output and X_names=input_names, Y_names=output_names
X,Y,X_names,Y_names = myScikitLearnDatasets.getXY()
# 5. Convert numpy array data to Pandas Dataframe
df_X,df_Y = createPandasDataFrame(X,Y,X_names,Y_names)
print("#---------- DATASET INFORMATION ------------#")
print("X Input or feature_names: ", X_names)
print("Y Output or target_names: ", Y_names)
print("Input X Shape: " , X.shape)
print("Output Y Shape: " , Y.shape)
print("Dataframe df_X Input Describe: \n", df_X.describe())
print("Dataframe df_Y Output Describe: \n", df_Y.describe())
print("#-------------------------------------------#")
# 6. Write Pandas dataframe df_X, df_Y to csv file
directory_path = os.path.join(os.getcwd(), "ScikitLearnDatasets")
writeDataFrameToCsv(df_X,df_Y,directory_path, dataset_name)
# ------------------------------------------------ #
# ----------- READ DATASET FROM CSV -------------- #
# Read previously saved dataset
# 1. Read csv dataset (examvle boston_X.csv and boston_Y.csv) and transform to pandas daframe
#dataset_name = "boston" # desired dataset name
#directory_path = os.path.join(os.getcwd(), "ScikitLearnDatasets") # dataset folder
df_X,df_Y = readDataFrameFromCsv(directory_path, dataset_name)
# ------------------------------------------------ #
# -------- Split data into train and test -------- #
# Split dataset into training and test set
X_train, X_test, Y_train, Y_test = train_test_split(df_X.values, df_Y.values, test_size=0.20, random_state=42)
# ------------------------------------------------ #
# -------------------- PCA ----------------------- #
# Principal component analysis (PCA) or dimensionality reduction
# Number of input is reduced while keeping overall dataset information
# 1. Covert numpy array to pandas dataframe
df_X_train = pd.DataFrame(data = X_train , columns=df_X.keys())
df_X_test = pd.DataFrame(data = X_test , columns=df_X.keys())
# 2. Initialize PCA (Principal Component Analysis)
n_components = 0.95 # 90% of the variance
mydimensionalityReduction = dimensionalityReduction(n_components)
# 3. Create PCA model (using input training data)
pcaModel,information_array, total_information = mydimensionalityReduction.fit(df_X_train)
print("#-------------- PCA ANALYSIS ---------------#")
print("Information for each new component: ", information_array, "%")
print("Total Information of the reduced dataset: ", total_information, " %")
# 4. Apply created PCA model to both training and test dataset
df_X_train_scaled = mydimensionalityReduction.transform(pcaModel,df_X_train)
df_X_test_scaled = mydimensionalityReduction.transform(pcaModel,df_X_test)
X_train_scaled = df_X_train_scaled.values
X_test_scaled = df_X_test_scaled.values
#print("Dataset X_train: ", X_train)
#print("Dataset X_train Reduced: ", X_train_scaled)
print("Number of inputs with PCA: ",X_train_scaled.shape[1])
print("Number of inputs without PCA: ",X_train.shape[1])
print("#-------------------------------------------#")
# --------------------------------------------------#
# -------- LINEAR REGRESSION WITH PCA DATA -------- #
# we use reduce input data
myModelPCA = LinearRegression()
trained_modelPCA = myModelPCA.train(X_train_scaled, Y_train)
Y_predPCA,R2_scorePCA, RMSE_scorePCA = myModelPCA.evaluate(X_test_scaled,Y_test,trained_modelPCA)
print("#----- LINEAR REGRESSION PCA RESULTS -------#")
print("w1,w2 .. wN : ",trained_modelPCA.coef_)
print("w0 : ", trained_modelPCA.intercept_)
print("Score Linear Regression PCA: ", "R2 Score: ", R2_scorePCA, " RMSE Score: ", RMSE_scorePCA)
print("#-------------------------------------------#")
#myModelPCA.plot(Y_test,Y_pred)
# ------------------------------------------------ #
# -------------- LINEAR REGRESSOR ---------------- #
# We use initial data
myModel = LinearRegression()
trained_model = myModel.train(X_train, Y_train)
Y_pred,R2_score, RMSE_score = myModel.evaluate(X_test,Y_test,trained_model)
print("#------- LINEAR REGRESSION RESULTS ---------#")
print("w1,w2 .. wN : ",trained_modelPCA.coef_)
print("w0 : ", trained_modelPCA.intercept_)
print("Score Linear regression without PCA: ", "R2 Score: ", R2_score, " RMSE Score: ", RMSE_score)
print("#-------------------------------------------#")
#myModel.plot(Y_test,Y_pred)
# ------------------------------------------------ #
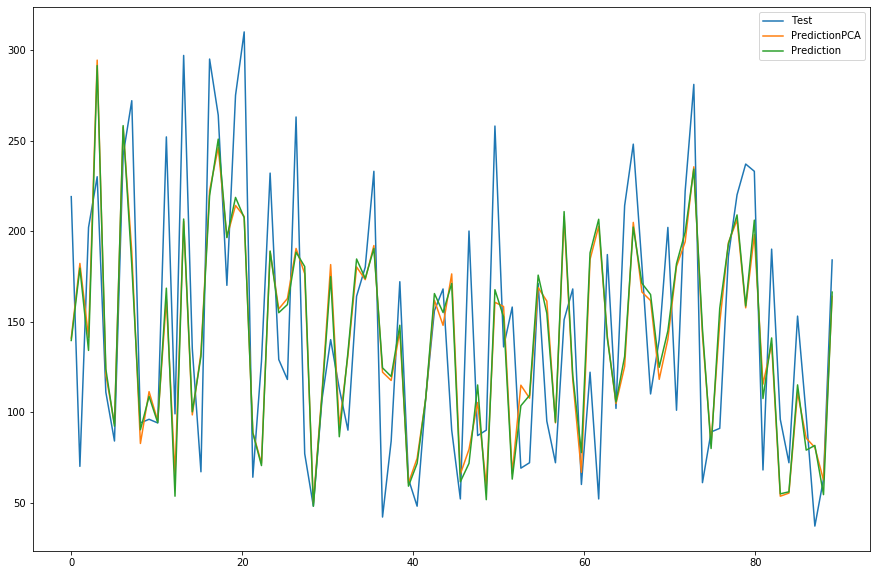
#----------------- COMPARISON -------------------- #
length = Y_pred.shape[0] # 20
index_bar = np.linspace(0,length,length)
plt.plot(index_bar, Y_test, label='Test')
plt.plot(index_bar, Y_predPCA, label='PredictionPCA')
plt.plot(index_bar, Y_pred, label='Prediction')
plt.legend()
plt.show()
# ------------------------------------------------ #
#---------- DATASET INFORMATION ------------#
X Input or feature_names: ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
Y Output or target_names: ['Desease-Progression']
Input X Shape: (442, 10)
Output Y Shape: (442,)
Dataframe df_X Input Describe:
age sex ... s5 s6
count 4.420000e+02 4.420000e+02 ... 4.420000e+02 4.420000e+02
mean -3.634285e-16 1.308343e-16 ... -3.830854e-16 -3.412882e-16
std 4.761905e-02 4.761905e-02 ... 4.761905e-02 4.761905e-02
min -1.072256e-01 -4.464164e-02 ... -1.260974e-01 -1.377672e-01
25% -3.729927e-02 -4.464164e-02 ... -3.324879e-02 -3.317903e-02
50% 5.383060e-03 -4.464164e-02 ... -1.947634e-03 -1.077698e-03
75% 3.807591e-02 5.068012e-02 ... 3.243323e-02 2.791705e-02
max 1.107267e-01 5.068012e-02 ... 1.335990e-01 1.356118e-01
[8 rows x 10 columns]
Dataframe df_Y Output Describe:
Desease-Progression
count 442.000000
mean 152.133484
std 77.093005
min 25.000000
25% 87.000000
50% 140.500000
75% 211.500000
max 346.000000
#-------------------------------------------#
#-------------- PCA ANALYSIS ---------------#
Information for each new component: [39.68814054 14.77973436 12.51654914 10.10869693 6.58293305 5.93511774
5.2036642 4.33649442] %
Total Information of the reduced dataset: 99.15133037867369 %
Number of inputs with PCA: 8
Number of inputs without PCA: 10
#-------------------------------------------#
#----- LINEAR REGRESSION PCA RESULTS -------#
w1,w2 .. wN : [[ 453.41998089 -244.95319406 372.8080337 524.14406459 -30.20353053
-252.44550156 125.2975691 34.12174383]]
w0 : [151.30071414]
Score Linear Regression PCA: R2 Score: 0.4557153915064335 RMSE Score: 53.7001159233466
#-------------------------------------------#
#------- LINEAR REGRESSION RESULTS ---------#
w1,w2 .. wN : [[ 453.41998089 -244.95319406 372.8080337 524.14406459 -30.20353053
-252.44550156 125.2975691 34.12174383]]
w0 : [151.30071414]
Score Linear regression without PCA: R2 Score: 0.45260660216173787 RMSE Score: 53.8532569849144
#-------------------------------------------#
Referenze utili¶
Extra : Come funzionano i dizionari in python¶
#---------------------------------------------------------------------
#---------------- Trasformare dizionari in Array --------- -----------
#---------------------------------------------------------------------
# Usiamo Le funzioni
# Importare i datasets
from sklearn import datasets
import numpy as np
iris = datasets.load_iris() # Load iris dataset
digits = datasets.load_digits() # Load digits dataset
boston = datasets.load_boston() # Load boston dataset
diabetes = datasets.load_diabetes() # Load diabetes dataset
linnerud = datasets.load_linnerud() # Load linnerud dataset
wine = datasets.load_wine() # Load wine dataset
breast_cancer = datasets.load_breast_cancer() # Load breast_cancer dataset
dataset_scelto = iris
def approccio_1(dataset_scelto):
# --------------------- Approccio 1
# Get dictionar keys, value
print(dataset_scelto.keys())
list_keys = []
list_values = []
for key in dataset_scelto:
list_keys.append(key)
print(key)
value = dataset_scelto[key]
list_values.append(value)
print("All keys inside array ", list_keys)
#print("All values inside array ", list_values)
# Convert list to numpy array
print("----------------------------------")
array_keys = np.asarray(list_keys)
array_values = np.array(list_values)
print(type(array_keys), array_keys.shape, array_keys[0].shape)
print(type(array_values), array_values.shape,array_values[0].shape)
# Going deeper inside data shape
print("----------------------------------")
for i in range(0,len(array_keys)):
if isinstance(array_values[i],np.ndarray):
print(array_keys[i], type(array_values[i]), array_values[i].shape )
else:
print(array_keys[i], type(array_values[i]))
# Other Useful Solutions
'''
for value in diabetes.values():
print(value)
for key, value in diabetes.items():
print(key, value)
'''
def approccio_2(dataset_scelto):
#--------------------- Approccio 2
# Convert a dictionary to an array of string
list_keys = list(dataset_scelto.keys())
list_values = list(dataset_scelto.values())
#print(list_keys)
print(type(list_keys))
#print(list_values)
print(type(list_values))
# Convert list as numpy narray
array_keys = np.asarray(list_keys)
array_values = np.array(list_values)
print(type(array_keys))
print(type(array_values))
# Covert back numpy ndarray to list
new_list_keys = array_keys.tolist()
new_list_values = array_values.tolist()
print(type(new_list_keys))
print(type(new_list_values))
# Check if the list are equal
if list_keys == new_list_keys and list_values==new_list_values:
print ("The lists are identical")
else :
print ("The lists are not identical")
print("-----------------------------")
print("-------- Approach 1 ---------")
print("-----------------------------")
approccio_1(dataset_scelto)
print("-----------------------------")
print("-------- Approach 2 ---------")
print("-----------------------------")
approccio_2(dataset_scelto)
-----------------------------
-------- Approach 1 ---------
-----------------------------
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
data
target
target_names
DESCR
feature_names
filename
All keys inside array ['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']
----------------------------------
<class 'numpy.ndarray'> (6,) ()
<class 'numpy.ndarray'> (6,) (150, 4)
----------------------------------
data <class 'numpy.ndarray'> (150, 4)
target <class 'numpy.ndarray'> (150,)
target_names <class 'numpy.ndarray'> (3,)
DESCR <class 'str'>
feature_names <class 'list'>
filename <class 'str'>
-----------------------------
-------- Approach 2 ---------
-----------------------------
<class 'list'>
<class 'list'>
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
<class 'list'>
<class 'list'>
The lists are identical
